Exponential functions and Euler's formula
$\newcommand\R{\mathbb{R}}\newcommand\C{\mathbb{C}}\newcommand\Z{\mathbb{Z}}\newcommand\Q{\mathbb{Q}}$
This post was driven by a desire to explain and prove Eulder's formula, \begin{equation}\label{euler} e^{i\theta} = \cos\theta + i\sin \theta, \end{equation} in a more conceptual way than the standard explanation using power series. Power series are still used as the key technical tool for proving the existence and uniqueness of exponential functions.
Acknowledgements. This was provoked by a Quanta Magazine article by Steven Strogatz on how to prove Euler's formula using power series. The discussion below was inspired by Michael Hutchings' observation that Euler's formula can be proved by solving an ordinary differential equation. I'd also like to thank Dan Lee, Keith Conrad, and my other Facebook friends for their comments and corrections.
Introduction
At first, even the meaning of the left side of Euler's formula \eqref{euler} is unclear. The standard approach is to use power series to define $e^{i\theta}$ and prove Euler's formula. The argument is outlined below. It is simple and elegant. I have, however, always found it unsatisfying, since the power series alone provides little intuition into what's going on.
Here, I provide an alternative approach that I find that is easier to understand intuitively. Moreover, it accomplishes much more. Using only calculus, it provides rigorous definitions of not only the exponential, sine, and cosine functions, but also the constants $\pi$ and $e$. From these definitions, it is straightforward to prove the fundamental properties of these functions, including Euler's formula.
It is worth noting that the standard way to define the sine and cosine functions requires the concept of an angle, in degrees or radians, but no rigorous definition is provided This in fact is not easy to do and rarely discussed at all in calculus textbooks. Here, we start with the definition of $e^{i\theta}$ and use it to define rigorously what the sine and cosine functions, as well as angles, are.
The exposition here does not require the use of power series. Power series are needed only for proving rigorously the existence of exponential functions. The details of this have been relegated to the Appendix.
Power series proof of Euler’s formula
Here is a brief outline of how to prove Euler's formula using power series. The starting point are the power series \begin{align} e^{x} &= \sum_{k=0}^\infty \frac{x^k}{k!} = 1 + x + \frac{x^2}{2!} +\cdots \label{taylor}\\ \sin x &= \sum_{k=0}^\infty (-1)^k\frac{x^{2k+1}}{(2k+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots \notag\\ \cos x &= \sum_{k=0}^\infty (-1)^k\frac{x^{2k}}{(2k)!} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} + \cdots. \notag \end{align} It follows by the ratio test that these series converge for every $x \in \R$. The key observation is that these power series also converge if $x$ is complex, extending the domains of these functions from $\R$ to $\C$. Euler's formula now follows by setting $x = i\theta$ in \eqref{taylor} and splitting the series into its real and imaginary parts, \begin{align*} e^{i\theta} &= \sum_{k=0} \frac{(i\theta)^k}{k!}\\ &= \sum_{k=0} (-1)^k \frac{\theta^{2k}}{(2k)!} + i\sum_{k=0} (-1)^k \frac{\theta^{2k+1}}{(2k+1)!}\\ &= \cos\theta + i\sin\theta. \end{align*} This is simple and elegant, but the proof provides little intuition to what is going on. Euler's formula appears magically.
Below is an alternative approach that I think elucidates how the exponential function of both real and imaginary numbers arise and why exponential of an imaginary number has a geometric interpretation. The explanation below requires only basic calculus. No knowledge of differential equations is needed. The appendix provides a rigorous discussion showing how to use power series to solve a simple ordinary differential equation. The uniqueness of the solution follows from basic properties of the integral.
Exponential function of a real number
We start by recalling what a real exponential function is.
Linear function
We start by with the definition of a linear function. A function $f: \R \rightarrow \R$ is linear if the change in output depends only on the change in input and not on the input itself. More precisely, for any change in input, $\Delta \ne 0$, there exists $c(\Delta) \in \R$ such that $$ f(x+\Delta) - f(x) = c(\Delta),\ \forall x \in \R $$ Observe that $c(0) = 0$. Therefore, if $f$ is assumed to be differentiable, then \begin{align*} f'(x) &= \lim_{\Delta\rightarrow 0} \frac{f(x+\Delta)-f(x)}{\Delta}\\ &= \lim_{\Delta\rightarrow 0} \frac{c(\Delta)-c(0)}{\Delta}\\ &= c'(0), \end{align*} which is a constant. If we set $m = c'(0)$ and $b = f(0)$, this implies that if $f$ is linear, then $$ f(x) = mx + b. $$ The converse also holds.
Exponential functions
An exponential function has a similar definition except that change in output is replaced by relative change in input. In other words, a function $E: \R \rightarrow \R$ is exponential if the percentage or relative change of $E$ depends only on the change in input and not on the input itself. More precisely, for any $\Delta \in \R$, there exists $C(\Delta)$ such that \begin{equation}\label{relative-change} \frac{E(x+\Delta)-E(x)}{E(x)} = C(\Delta). \end{equation} Observe that $C(0) = 0$. From this, it follows that, if $E$ is differentiable, then \begin{align*} \frac{E'(x)}{E(x)} &= \lim_{\Delta\rightarrow 0}\frac{E(x+\Delta)-E(x)}{E(x)\Delta}\\ &= \lim_{\Delta\rightarrow 0}\frac{C(\Delta)-C(0)}{\Delta}\\ &= C'(0) \end{align*} This implies that $C(\Delta)$, as a function of $\Delta$, is differentiable at $\Delta = 0$, and \begin{equation}\label{exponential} E'(x) = \kappa E(x), \end{equation} where $\kappa = C'(0)$ is a constant.
Any function $E$ on a nonempty connected interval $I$ that satisfies \eqref{exponential} for some constant $\kappa$ is called an exponential function. Observe that if $\kappa = 0$, then $E$ is a constant function.
Existence of exponential functions
The following is proved in the appendix:
Properties of exponential functions
Product of exponential functions is exponential: Let $E_1$ and $E_2$ be exponential functions that satisfy $$ E_1' = \kappa_1E_1 \text{ and } E_2' = \kappa_2E_2. $$ If $E_3 = E_1E_2$, then \begin{align*} E_3' &= E_1'E_2 + E_1E_2'\\ &= (\kappa_1+\kappa_2)E_1E_2\\ &= \kappa_3 E_3, \end{align*} where $\kappa_3 = \kappa_1+\kappa_2$.
A special case is when $$ E_1'=\kappa E_1\text{ and }E_2=-\kappa E_2$$ on a nonempty connected open interval $I$. In that case, the product $E_1E_2$ is a constant function. This leads to the following:
An exponential function is either always or never zero: If $E' = \kappa E$ on a nonempty connected open interval $I$, then either $E=0$ on $I$ or $E$ is never zero on $I$.
Proof: Suppose there exists $t_0 \in I$ such that $E(t_0) = e_0 \ne 0$. Let $E_2$ be the exponential function given by $$E_2' = -\kappa E_2\text{ and }E_2(t_0) = 1. $$ This implies that for any $t \in I$, $$ E(t)E_2(t) = e_0. $$ Therefore, $E(t) \ne 0$ for each $t \in I$.
The properties above imply the uniqueness of a solution to \eqref{ode}. See the Appendix for a proof.
Standard exponential functions
Given $\kappa \in \R$, let $e_\kappa: \R \rightarrow \R$ denote the unique function such that \begin{equation}\label{ode1} e_\kappa' = \kappa e_\kappa\text{ and }e_\kappa(0) = 1 \end{equation}
Observe that if $E(x) = e_1(\kappa x)$, then $$ E'(x)=\kappa e_1'(\kappa x) = \kappa e_1(\kappa x) = \kappa E\text{ and }E(0)=1. $$ By the uniqueness of a solution to \eqref{ode1}, it follows that $E = e_\kappa$ and therefore $$ e_\kappa(x) = e_1(\kappa x),\ \forall x \in \R. $$
An important property of a standard exponential function is the following:
\begin{equation}\label{translation} e_\kappa(s+t) = e_\kappa(s)e_\kappa(t) \end{equation} This follows from the fact that if $s$ is held fixed, then the two sides of the equation are solutions to \eqref{ode} and therefore have to be equal.
Euler’s constant $e$
We define Euler’s constant to be \(e = e_1(1).\)
It follows by \eqref{translation} that for any nonnegative integer $k$, $$ e_1(k+1) = e_1(k). $$ By induction and that $e_1(0)=0$, it follows that $$ e_1(k) = e^k. $$ Also, since $$ 1 = e_1(0) = e_1(k+(-k)) = e_1(k)e_1(-k), $$ it follows that for any positive integer $k$, $$ e_1(-k) = e^{-k}. $$ Therefore, for any integer $k$, $$ e_1(k) = e^k. $$
For any rational number $\frac{n}{d}$, where $n$ is an integer and $d$ is a positive integer, \begin{align*} e^n &= e_1(n)\\ &= e_1\left(\frac{n}{d}+\cdots+\frac{n}{d}\right)\\ &= \left(e_1\left(\frac{n}{d}\right)\right)^d \end{align*} It follows that \begin{align*} e_1\left(\frac{n}{d}\right) &= (e^n)^{\frac{1}{d}} = e^{\frac{n}{d}}. \end{align*} In short, for any rational $r$ $$ e_1(r) = e^r. $$
These properties justify the following definition: For any $x \in \R$, we denote the standard exponential function by $$ e^x = e_1(x). $$ Note that if $x$ is irrational, this is the definition of $e^x$. This function satisfies the following properties: \begin{align*} e^x &> 0,\ \forall x \in \R\\ e^0 &= 1\\ e^{x+y} &= e^xe^y,\ \forall x,y \in \R. \end{align*}
Moreover, any exponential function $E: \R \rightarrow \R$ can be written as $$ E(t) = e_0e^{\kappa t}, $$ where $e_0 = E(0)$ and $\kappa = E'/E$ are constants.
Exponential of an imaginary number
Definition
Now suppose you want to extend the definition of $e^t$ to $t \in \C$. Let us focus first on the case $t = i$. One could try to define $$ e^i = e_1(i). $$ But this is problematic, because it would mean trying to solve \eqref{ode} with respect to an independent variable $t$ that is complex instead of real. A better approach is to use \eqref{ode} as a template and define $$ e^i = e_i(1), $$ where $e_i$ satisfies the equation \begin{equation} e_i' = ie_i\text{ and }e_i(0) = 1. \label{ode2} \end{equation} By Theorem A in the appendix that there is a unique solution $e_i: \R \rightarrow \C$ to \eqref{ode2}. Moreover, for any $t_1, t_2 \in \R$, $$ e_i(t_1 + t_2) = e_i(t_1)e_i(t_2), $$ which justifies writing, for any $t \in \R$, $$ e_i(t) = e^{it}. $$
Geometric properties of the exponential of an imaginary number
We now want to understand the function $e^{it}$ better. An unexpected twist is that geometry and trigonometry naturally appear in the description of this function.
If we write $e_i(t) = x(t) + iy(t)$, then \eqref{ode2} is equivalent to the system \begin{align}\label{ode3} (x',y') &= (-y,x)\text{ and }(x(0),y(0)) = (1,0). \end{align} A solution to this satisfies $$ (x',y')\cdot (x,y) = x'x + y'y = -yx + xy = 0. $$ Therefore, $(x(t),y(t))$, $t \in \R$, is a parameterized curve whose velocity vector $$ v = (x', y') $$ is always orthogonal to the position vector $(x,y)$. It follows easily from \eqref{ode3} that \begin{align*} x^2 + y^2 &= 1\\ (x')^2+(y')^2 &= 1. \end{align*} The first equation says the curve always lies on the unit circle centered at the origin. The second says that the speed, which is the norm of the velocity vector, is always equal to $1$. Putting this all together, we see that the solution is a unit speed parameterization of the circle.
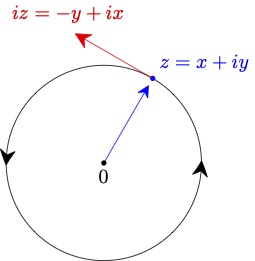
Since the parameterization has unit speed, it is intuitively clear that, as $t$ increases, the solution $(x(t),y(t))$ to \eqref{ode3} goes around the entire circle at least once. In particular, there exists $\tau > 0$ such that $$ e_i(\tau) = e_i(0) = 1. $$ A rigorous proof of this is provided in the Appendiex. The translation invariance of \eqref{ode2} implies that for any $t \in \R$, $$ e_i(t + \tau) = e_i(t)e_i(\tau) = e_i(t). $$ A function with this property is called periodic.
Definition of $\pi$
Let $\tau$ be the smallest positive constant such that $$ e_i(\tau) = 1. $$ The constant $\pi$ is defined to be $$ \pi = \frac{\tau}{2}. $$ For each $t \in [0,2\pi]$, $$ e_i(t) = x(t) + iy(t) $$ is the point reached by traveling at unit speed along the circle staring from $(1,0)$, we can define the length of the arc from $(1,0)$ to $(x(t),y(t))$, where $0 \le t < 2\pi$, to be $t$. In particular, the circumference of the circle, which is defined to be the length of the full circle, is $2\pi$.
The angle in radians from $(1,0)$ to the point $(x,y)$ on the unit circle is defined to be the length of the arc from $(1,0)$ to $(x,y)$ and therefore the unique $t \in [0,2\pi)$ such that $$ e^{it} = x + iy. $$
Definitions and properties of trig functions
We can now define the basic trig functions to be, for any $\theta \in \R$, \begin{align*} \cos\theta &= x(\theta)\\ \sin\theta &= y(\theta), \end{align*} where $$ e^{i\theta} = x(\theta) + iy(\theta). $$ In other words, $$ e^{i\theta} = \cos\theta + i\sin\theta. $$ Therefore, the sine and cosine functions are defined using Euler's formula.
Straightforward consequences of everything above include $$ (\sin\theta)^2 + (\cos\theta)^2 = 1, $$ Euler's formula $$ e^{i\theta} = \cos\theta + i\sin\theta, $$ and the standard differentiation formulas, \begin{align*} \frac{d}{d\theta}(\sin\theta) &= \cos\theta\\ \frac{d}{d\theta}(\cos\theta) &= -\sin\theta. \end{align*} It is also straightforward to use the symmetries of \eqref{ode2} to derive all of the basic properties of the sine and cosine functions, such as: \begin{align*} \sin(n\pi) &= 0\\ \sin\left(\frac{\pi}{2}+2\pi n\right) &= 1\\ \sin\left(\frac{3\pi}{2}+2\pi n\right) &= -1\\ \cos(2n\pi) &= 1\\ \cos((2n+1)\pi) &= -1\\ \cos\left(\frac{\pi}{2}+n\pi\right) &= 0, \end{align*} where $n$ is any integer. Many trigonometric identities also follow easily by raising $e^{i\theta}$ to integer and rational powers.
Exponential of a complex number
Finally, it is now obvious how to define the exponential of a complex number $z$, namely $$ e^{z} = e_z(1), $$ where $e_z$ is the unique solution to the ODE \begin{equation}\label{ode4} e_z' = ze_z\text{ and }e_z(0) = 1. \end{equation} Again, it is straightforward to show that $$ e^{z_1+z_2} = e^{z_1}e^{z_2} $$ and, in particular, $$ e^{x+iy} = e^xe^{iy} = e^x(\cos y + i\sin y).. $$
Summary
We have succeeded in using only calculus to obtain the following in a natural and intuitive way:
- Definitions of the constants $e$ and $\pi$
- Definitions and fundamental properties of $e^z$ for any $z \in \C$
- Definitions of $\sin\theta$ and $\cos\theta$ for any $\theta \in \R$
- Euler's formula
Appendix
Existence of a solution to \eqref{ode}, \eqref{ode2}, or \eqref{ode4}
Since \eqref{ode} and \eqref{ode2} are special cases of \eqref{ode4}, it suffices to prove the following:
We use power series to prove that a solution to \eqref{ivp} exists.
Consider the power series $$ E(t) = \sum_{k=0} c_kt^k. $$ If $E$ satisfies the equation \eqref{ivp}, then that $c_0 = e_0$ and $$ \sum_{k=0}^\infty (k+1)c_{k+1}t^k = \sum_{k=0}^\infty \kappa c_kt^k, $$ which implies that for each $k \ge 0$, $$ c_{k+1} \frac{\kappa }{k+1}c_k. $$ By induction, we see that $$ c_k = e_0\frac{\kappa ^k}{k!}, $$ Therefore, the power series for $E$ is $$ e_0\sum_{k=0}^\infty \frac{(\kappa t)^k}{k!}. $$ It is easily checked that by the ratio test for series, the series, for any fixed $t \in \R$, converges absolutely. We can therefore define $$ E(t) = e_0\sum_{k=0}\frac{(\kappa t)^k}{k!}. $$
It remains to show that $E$ really does satisfy the \eqref{ivp}. First, we derive the power series for $E'$ as follows: \begin{align*} E'(x) &= \lim_{y\rightarrow x} \frac{E(y)-E(x)}{y-x}\\ &= \lim_{y\rightarrow x} \frac{1}{y-x}\left(e_0\sum_{k=0}^\infty \frac{(\kappa y)^k}{k!} - e_0\sum_{k=0}^\infty \frac{(\kappa x)^k}{k!}\right)\\ &= e_0\lim_{y\rightarrow x} \sum_{k=0}^\infty \frac{1}{k!}\left(\frac{(\kappa y)^k-(\kappa x)^k}{y-x}\right)\\ &= e_0\lim_{y\rightarrow x} \sum_{k=1}^\infty \frac{\kappa^k}{k!}(y^{k-1}+y^{k-2}x + \cdots + yx^{k-2} + x^{k-1})\\ &= e_0\sum_{k=1}^\infty \frac{\kappa^k}{k!}kx^{k-1}\\ &= \kappa e_0\sum_{k=0}^\infty \frac{(\kappa x)^k}{k!}\\ &= \kappa E. \end{align*} Since, by the ratio test, all of the series in the calculation above converge absolutely, it is a valid calculation and therefore $$ E' = \kappa E. $$
Uniqueness of a solution to \eqref{ode}, \eqref{ode2}, or \eqref{ode4}
The proof of existence already implies that \eqref{ode4} has a unique power series solution. However, we want to prove uniqueness assuming only that the solution is differentiable.
We have already shown that if $e_0=0$, then the only solution to \eqref{ivp2} is the zero function. On the other hand, if $e_0 \ne 0$, then $E=E_2-E_1$ satisfies \eqref{ivp2} with $e_0=0$. Therefore, $E$ is the zero function and $E_2=E_1$.
A solution to \eqref{ode3} goes around the whole circle
Lemma. Let $C = \{ (x,y) \in \R^2:\ x^2+y^2=1\}$. Let $(x,y): \R \rightarrow C$ be the unique solution to \begin{align}\label{ode5} (x',y') &= (-y,x)\\ \label{initial} (x(0),y(0)) &= (1,0). \end{align}
Then there exists $\tau > 0$ such that $$ \left.(x,y)\right|_{[0,\tau)}: [0,\tau) \rightarrow C $$ is a bijection and $(x(\tau),y(\tau))= (x(0),y(0))$.
Relative Change in Output of an Exponential Function
For any function $E$ satisfying \eqref{ode} and any $x, \Delta \in \R$, \begin{align*} E(x+\Delta)-E(x) &= e_0e_\kappa(x+\Delta) - e_0e_\kappa(x)\\ &= e_0(e_\kappa(x)e_\kappa(\Delta) - e_\kappa(x))\\ &= e_0e_\kappa(x)(e_\kappa(\Delta) - 1)\\ &= E(x)c(\Delta), \end{align*} where $$ c(\Delta) = e_\kappa(\Delta) - 1. $$ From this, it follows that a differentiable function $E$ satisfies \eqref{relative-change} if and only if it satisfies \eqref{ode}.